Soal
Diberikan dua buah fungsi masing-masing f(x) dan g(x) berturut-turut adalah:
f(x) = 3x + 2
g(x) = 2 − x
Tentukan:
a) (f o g)(x)
b) (g o f)(x)
Pembahasan
Data:
f(x) = 3x + 2
g(x) = 2 − x
a) (f o g)(x)
"Masukkan g(x) nya ke f(x)"
sehingga:
(f o g)(x) = f ( g(x) )
= f (2 − x)
= 3(2 − x) + 2
= 6 − 3x + 2
= − 3x + 8
b) (g o f)(x)
"Masukkan f (x) nya ke g (x)"
sehingga:
(g o f)(x) = g ( f (x) )
= g ( 3x + 2)
= 2 − ( 3x + 2)
= 2 − 3x − 2
= − 3x
Soal
Diberikan dua buah fungsi:
f(x) = 3x2 + 4x + 1
g(x) = 6x
Tentukan:
a) (f o g)(x)
b) (f o g)(2)
Pembahasan
Diketahui:
f(x) = 3x2 + 4x + 1
g(x) = 6x
a) (f o g)(x)
= 3(6x)2 + 4(6x) + 1
= 108x2 + 24x + 1
b) (f o g)(2)
(f o g)(x) = 108x2 + 24x + 1
(f o g)(2) = 108(2)2 + 24(2) + 1
(f o g)(2) = 432 + 28 + 1 = 461
Soal
Diketahui f(x) = x2 + 1 dan g(x) = 2x − 3, maka (f o g)(x) = ....
A. 4x2 − 12x + 10
B. 4x2 + 12x + 10
C. 4x2 − 12x − 10
D. 4x2 + 12x − 10
E. − 4x2 + 12x + 10
(Dari soal Ebtanas Tahun 1989)
Pembahasan
f(x) = x2 + 1
g(x) = 2x − 3
(f o g)(x) =.......?
Masukkan g(x) nya ke f(x)
(f o g)(x) =(2x − 3)2 + 1
(f o g)(x) = 4x2 − 12x + 9 + 1
(f o g)(x) = 4x2 − 12x + 10
Soal
Diketahui fungsi f(x) = 3x − 1 dan g(x) = 2x2 + 3. Nilai dari komposisi fungsi (g o f)(1) =....
A. 7
B. 9
C. 11
D. 14
E. 17
(Dari soal UN Matematika SMA IPA - 2010 P04)
Pembahasan
Diketahui:
f(x) = 3x − 1 dan g(x) = 2x2 + 3
(g o f)(1) =.......
Masukkan f(x) nya pada g(x) kemudian isi dengan 1
(g o f)(x) = 2(3x − 1)2 + 3
(g o f)(x) = 2(9x2 − 6x + 1) + 3
(g o f)(x) = 18x2 − 12x + 2 + 3
(g o f)(x) = 18x2 − 12x + 5
(g o f)(1) = 18(1)2 − 12(1) + 5 = 11
Soal
Diberikan dua buah fungsi:
f(x) = 2x − 3
g(x) = x2 + 2x + 3
Jika (f o g)(a) = 33, tentukan nilai dari 5a
Pembahasan
Cari (f o g)(x) terlebih dahulu
(f o g)(x) = 2(x2 + 2x + 3) − 3
(f o g)(x) = 2x2 4x + 6 − 3
(f o g)(x) = 2x2 4x + 3
33 = 2a2 4a + 3
2a2 4a − 30 = 0
a2 + 2a − 15 = 0
Faktorkan:
(a + 5)(a − 3) = 0
a = − 5 atau a = 3
Sehingga
5a = 5(−5) = −25 atau 5a = 5(3) = 15
Bagaimana jika yang diketahui adalah rumus (f o g)(x) atau (g o f)(x) nya kemudian diminta untuk menentukan f(x) atau g(x) nya, seperti contoh berikutnya:
Soal
Diketahui :
(f o g)(x) = − 3x + 8
dengan
f(x) = 3x + 2
Tentukan rumus dari g(x)
Pembahasan
f(x) = 3x + 2
(f o g)(x) = f (g(x))
− 3x + 8 = 3(g(x)) + 2
− 3x + 8 − 2 = 3 g(x)
− 3x + 6 = 3 g(x)
− x + 2 = g(x)
atau
g(x) = 2 − x
Tengok lagi contoh nomor 1, dimana f(x) = 3x + 2 dan g(x) = 2 − x akan menghasilkan (f o g)(x) = − 3x + 8
Soal
Diberikan rumus komposisi dari dua fungsi :
(g o f)(x) = − 3x
dengan
g(x) = 2 − x
Tentukan rumus fungsi f(x)
Pembahasan
(g o f)(x) = − 3x
(g o f)(x) = g(f(x))
− 3x = 2 − (f(x))
− 3x = 2 − f(x)
f(x) = 2 + 3x
atau
f(x) = 3x + 2
1. Diketahui (f o g)(x) = x + 1 dan f(x-2) = (x – 1)/(x – 2). Maka nilai dari g-’ (2) [dibaca: g invers 2] adalah…
Penyelesaian:
f(x – 2) = (x – 1)/(x – 2)
Inverskan x-2 agar ditemukan nilai dari f(x)
y = x – 2
x = y + 2 <—-> y = x + 2 maka:
f(x) = [(x + 2) - 1]/[(x + 2) - 2]
f(x) = (x + 1)/x
(f o g)(x) = f(g(x))
f(g(x)) = x + 1
[g(x) + 1]/g(x) = x + 1
g(x) + 1 = (x + 1). g(x)
g(x) + 1 = x.g(x) + g(x)
g(x) – x.g(x) -g(x) = -1
-x.g(x) = -1
g(x) = 1/x
g(x) = 1/x
y = 1/x
x = 1/y, maka:
g-’(x) = 1/x
Jadi, nilai dari g-’(2) adalah = 1/x = 1/2.
2. Diketahui f(3 + 2x) = 4 – 2x + x². maka f(x) = ….?
Penyelesaian:
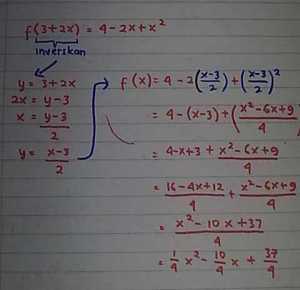 Jadi f(x) = 1/4 x² – 10/4x + 37/4
Jadi f(x) = 1/4 x² – 10/4x + 37/4
3. Diketahui f(x) = x³ + 4 dan g(x) = 2sinx. Nilai dari (f o g)(-90) adalah…
Penyelesaian:
(f o g)(x) = f(g(x))
= (g(x))³ + 4
= (2sinx)³ + 4
= 8sin³x + 4
Jadi, ( f o g) (-90) adalah
= 8sin³(-90) + 4
= 8.(-1) + 4
= -8 + 4 = -4.
4. Diketahui g(x) = (x² + 2x – 3)/4. Maka g-’(x) adalah…
Penyelesaian:
Perhatikan penyebutnya, untuk mencari invers sebuah fungsi kuadrat, salah satu caranya adalah mengubah persamaan umum kuadrat menjadi bentuk kuadrat sempurna. Maka:
= x² + 2x – 3
= x² + 2x + 1 – 1 – 3
= (x + 1)² – 4
Jadi,
g(x) = (x² + 2x – 3)/4
g(x) = [(x + 1)² - 4]/4
y = [(x + 1)² - 4]/4
4y = [(x + 1)² - 4]
(x + 1)² = 4y + 4
(x + 1)² = 4(y + 1)
x + 1 = √4(y + 1)
x + 1 = ±2 √(y + 1)
x = -1 ±2 √(y + 1)
g-’(x) = -1 ±2 √(x + 1)
5. Diketahui g(x) = px + q dan (g o g)(x) = 16x – 15 maka nilai p dan q adalah…
Penyelesaian:
(g o g)(x) = g(g(x))
16x – 15 = p(g(x)) + q
16x – 15 = p(px + q) + q
16x – 15 = p²x + pq + q
Cocokkan sesuai dengan variabel/konstantanya.
16x = p²x dan -15 = pq + q
Kemudian mencari nilai p dan q nya.
16x = p²x
16 = p²
p = √16 ——> p = ± 4.
Jika p = 4 maka q =
-15 = 4q + q
-15 = q(4 + 1)
q = -15/5 = -3
Jika p = -4 maka q =
-15 = -4q + q
-15 = q(-4 + 1)
q = -15/-3 = 5
Jadi, nilai p dan q adalah (4 dan -3) atau (-4 dan 5).
Penyelesaian:
f(x – 2) = (x – 1)/(x – 2)
Inverskan x-2 agar ditemukan nilai dari f(x)
y = x – 2
x = y + 2 <—-> y = x + 2 maka:
f(x) = [(x + 2) - 1]/[(x + 2) - 2]
f(x) = (x + 1)/x
(f o g)(x) = f(g(x))
f(g(x)) = x + 1
[g(x) + 1]/g(x) = x + 1
g(x) + 1 = (x + 1). g(x)
g(x) + 1 = x.g(x) + g(x)
-x.g(x) = -1
g(x) = 1/x
g(x) = 1/x
y = 1/x
x = 1/y, maka:
g-’(x) = 1/x
Jadi, nilai dari g-’(2) adalah = 1/x = 1/2.
2. Diketahui f(3 + 2x) = 4 – 2x + x². maka f(x) = ….?
Penyelesaian:
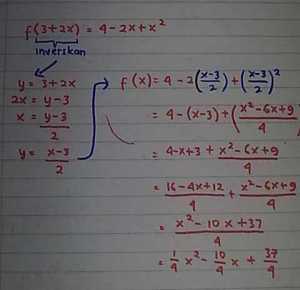 Jadi f(x) = 1/4 x² – 10/4x + 37/4
Jadi f(x) = 1/4 x² – 10/4x + 37/43. Diketahui f(x) = x³ + 4 dan g(x) = 2sinx. Nilai dari (f o g)(-90) adalah…
Penyelesaian:
(f o g)(x) = f(g(x))
= (g(x))³ + 4
= (2sinx)³ + 4
= 8sin³x + 4
Jadi, ( f o g) (-90) adalah
= 8sin³(-90) + 4
= 8.(-1) + 4
= -8 + 4 = -4.
4. Diketahui g(x) = (x² + 2x – 3)/4. Maka g-’(x) adalah…
Penyelesaian:
Perhatikan penyebutnya, untuk mencari invers sebuah fungsi kuadrat, salah satu caranya adalah mengubah persamaan umum kuadrat menjadi bentuk kuadrat sempurna. Maka:
= x² + 2x – 3
= x² + 2x + 1 – 1 – 3
= (x + 1)² – 4
Jadi,
g(x) = (x² + 2x – 3)/4
g(x) = [(x + 1)² - 4]/4
y = [(x + 1)² - 4]/4
4y = [(x + 1)² - 4]
(x + 1)² = 4y + 4
(x + 1)² = 4(y + 1)
x + 1 = √4(y + 1)
x + 1 = ±2 √(y + 1)
x = -1 ±2 √(y + 1)
g-’(x) = -1 ±2 √(x + 1)
5. Diketahui g(x) = px + q dan (g o g)(x) = 16x – 15 maka nilai p dan q adalah…
Penyelesaian:
(g o g)(x) = g(g(x))
16x – 15 = p(g(x)) + q
16x – 15 = p(px + q) + q
16x – 15 = p²x + pq + q
Cocokkan sesuai dengan variabel/konstantanya.
16x = p²x dan -15 = pq + q
Kemudian mencari nilai p dan q nya.
16x = p²x
16 = p²
p = √16 ——> p = ± 4.
Jika p = 4 maka q =
-15 = 4q + q
-15 = q(4 + 1)
q = -15/5 = -3
Jika p = -4 maka q =
-15 = -4q + q
-15 = q(-4 + 1)
q = -15/-3 = 5
Jadi, nilai p dan q adalah (4 dan -3) atau (-4 dan 5).
Makasih yaaaa
BalasHapusAda pembahasan soalnya yang gak dimengerti kk , boleh jelaskan ? Soal no 3 ( dari soal ebtanas tahun 1989 )
BalasHapusKk, mau tanya nih .klo soalnya kaya gini gimana ,ya. F(x) =4-3x dan g (x) =x²+2,jawablah (f.g) (x)...
BalasHapus(fog)(x)=f(g(x))
Hapus=f(X2+2)
=4-3(X2+2)
=4-3x2+6
=10-3x2.
kak saya mau tanya ni, f(x) = 2x-3 g o f(x) = 4x²-2x+6 yg di cari itu g(x)
BalasHapusterima kasih
Dik:f(x)=2x-3,(fog)(x)=4x2-2x+6,maka : g(x)=
HapusJawab:f(g(x))=4x2-2x+6
2g(x)-3=4x2-2x+6
2g(x). =4x2-2x+6+3
2g(x). =4x2-2x+9
g(x). =4x2/2-2x/2+9/2
Matur thankyou
BalasHapusKak mau nanya
BalasHapusdiketahui:
(F○g)(x)=x^2 -14x + 45
F(x) = x^2 + 2x -3
Ditanya: g(x)=....?
Diketahuip
BalasHapusDiketahuip
BalasHapusBagaimana jika dik f(x) g(x) dan h(x) dan yang ditanyakan hogof(x)
BalasHapusAda soal tentang mencari gof(x) pecahan ga?
BalasHapusAda soal tentang mencari gof(x) pecahan ga?
BalasHapusJika f(x) = x+2 dan g(x)=2x-3,maka (gof)(x)?
HapusTolong dijawab yah
Kk kalo misalnya soalnya gini gimana kak? Diketahui f(x) = 2x+p g(x) = 3x+120 ditanya nilai p nya gimana kak?
BalasHapusKa kalo bentuk soal nya yang gini
BalasHapusJika invers fungsi f(x) adalah f-¹(x) 2x/3-x maka f(3)=
Kak kalau soal nya gini gimana cara penyelesaian nya kak
BalasHapusJika g(x)=x2ataukuadrat+1
Tentukanlah:
a. g3(x)
b. (gogog)(x)
Ka saya mau tanya nih
BalasHapusDiketahui:
f(x) =1-2x
(g•f)(x) =4x²-6x+3
Tentukan: g(x) dan nilai (f•g)(4)
Ka saya mau tanya tolong di jawab ya
BalasHapusDiketahui:
f(X) = 1-2x
(g•f)(x)= 4x²-6x+3
Tentukan
a.g(x)
b.nilai (f•g)(4)
Kk mau nanyak nih jika g(x)=2x-1 dan (f°g) (x) =4x+2x-3,maka f(x) adalah?
BalasHapusTolong bantu dong kak
Kalau soal ini bagaimana kalau menjawabnya?
BalasHapusDiketahui:f(x)=x²-4
g(x)=2x+3
h(x)=x+5/3-x
Ditanya :tentukan rumus f bundaran g,f bundaran h,g bundaran h,f bundaran g bundaran h,h budaran g bundaran f
TOLONG DI JAWAB YA...
Kak saya mau nanyak klok
BalasHapusDiketahuif(x)=3x²+5
g(x)=2x+7
Ditanya:a.(f•g)(x)
b.(g•f)(x)
Kak saya mau nanya kak
BalasHapusDiketahui :
(fog)^-1 (x)= 4+2x
(hot) (x)= x-3
Ditanya:
(gof)^-1 (-12)
Gimana ya kak caranya
Saya mau ny g(×) dan (fog)(×)ײ-3×+2 dit=tentukan nilai f(0)
BalasHapusBoleh tau caranya yang pake akar?
BalasHapusKakak aku mau tanya doang soal ini diketahui p(x) x dan q (x) 2x+1 maka nilai dari poq (0)
BalasHapusKk mau nanya
BalasHapusDik:f(x)=2x²-3+1
g(x)=x+2
Dit:a.(fog)(x)=
b.(gof)(x)=
C.(fog)(2)=
d.(gof)(-1)=
Kak mau tanya ini tolong di jawab yah
BalasHapusDik : f(x) : 3x
g(x) : 2x + 1
h(x) : x - 5
Ditanya : a. f(2)
b . (fog) (x)
c . (fog) (-2)
d . (foh) (x)
e . (goh) (5)
Ka mau tanya cara kkrja
BalasHapusDi ketahui f(x)=x + 6 dan g(x)=x - 5.Tentukan kompisi-komposi berikut:
g o g
Diketahui fungsi f(X)= x²+5,9(X)=X+4.tentukanlah fungsi
BalasHapusa.(f-g)
B.(f:g)
Diketahui fungsi f(x)=x^2 - 1 g(x)=2x-3 . Tentukan lah fungsi
BalasHapusa. fog (x)
b. gof (x)
c. Fog (1)
d. gof (1)